MIST
Magnetosphere, Ionosphere and Solar-Terrestrial
Polytropic Analysis of Large-scale Compressive Fluctuations in the Solar Wind: Fluid and Kinetic Behavior
By Ioannou Charalambos (University College London)
Large-scale compressive plasma fluctuations are a minor component of solar wind turbulence but still significantly shape the turbulent cascade. They perturb the pressure and internal energy of the plasma, and thus influence the evolution of the solar wind’s bulk properties (i.e., density, temperature) and can subject the plasma to various large-scale temperature anisotropy and beam instabilities. Observations of the solar wind show that these fluctuations are typically characterized by an anticorrelation between the plasma density and the magnitude of the magnetic field, and thus share polarization properties with slow waves. The nature of the slow modes in the solar wind with respect to the polarization properties of the plasma has been found to be in better agreement with the magnetohydrodynamic (MHD) slow mode predictions compared to that of the kinetic slow mode.
The polytropic behaviour of the plasma in compressive fluctuations may provide further insight into the nature of the slow mode, since the MHD, Chew–Goldberger–Low (CGL), and kinetic slow modes predict different proton polytropic indices (γ). Using Solar Orbiter observations, we determine the effective polytropic index of protons and electrons for two compressive fluctuations events, and compare them with the theoretical expectations of MHD, CGL, and kinetic slow modes. The first event exhibits characteristics of the MHD slow mode (γp ≈ 1.7) while the second event is more consistent with the kinetic slow mode (γp ≈ 3). We show that the Coulomb collisionality of the first event is stronger than the second event which may explain the different behaviour between the two events. Additionally, multiscale analysis shows that nature of the two events does not change significantly with scale. However, a scale dependence is observed for both events that suggests that kinetic effects become more prominent at smaller scales.

Polytropic index results for protons and electrons in the first (left) and second (right) compressive fluctuations events. R_p is the Pearson correlation coefficient. Panels (a)–(c) show the proton results and panels (d)–(f) show the electron results. Panels (a) and (d) show the parallel, panels (b) and (e) the perpendicular, and panels (c) and (f) the isotropic polytropic index results. The colour of the data points represents the time instance of the corresponding measurement in the interval. The first event shares characteristics with the MHD slow mode with an isotropic proton polytropic index of γ_p ≈ 5/3, while the second event shares characteristics with an Ion Acoustic wave with a parallel proton polytropic index of γ_(∥p) ≈ 3
See publication for details:
Ioannou, C. et al. (2025) ‘Polytropic Analysis of Large-scale Compressive Fluctuations in the Solar Wind: Fluid and Kinetic Behavior’, The Astrophysical Journal, 988(2), p. 253. Available at: https://doi.org/10.3847/1538-4357/adeb7b
Announcement of New MIST Council 2025
We are very pleased to announce the following members of the community have been elected to MIST Council:
- Gemma Bower (University of Leicester), MIST Councillor
- Tom Elsden (University of St Andrews), MIST Councillor
- Cameron Patterson (Lancaster University), MIST Councillor
- Fiona Ball (University of Southampton), Student Representative
They will begin their terms in July 2025.
We thank outgoing MIST Council members: Maria Walach, Chiara Lazzeri and Emma Woodfield. Andy Smith will remain on council a little longer as a co-opted member to cover Rosie Johnson's maternity leave.
The current composition of Council can be found on our website (https://www.mist.ac.uk/community/mist-council).
Ubiquitous threshold for coherent structures in solar wind turbulence
By Alina Bendt (University of Warwick)
The solar wind may be heated by turbulence. Coherent structures which are one possible mediating mechanism of the turbulent cascade may dissipate energy. The partial variance increment (PVI) is routinely used to characterize and identify coherent structures. Previously the threshold beyond which fluctuations may be coherent structures was identified by comparisons to a Gaussian distribution. We compare wavelet decompositions with the Haar and 10th-order Daubechies wavelets to determine the threshold from the physical character of the fluctuations. These wavelets are sensitive to sharp changes and oscillations in the time series respectively. Comparisons of the fluctuation distributions obtained from these two wavelets reveal a core and tail., the latter is dominated by coherent structures. The transition from core to tail identifies the PVI threshold. This threshold coincides with the PVI value where the PVI distributions obtained from the Haar and Db10 wavelets start to depart from each other. We find a single value for the threshold in each the kinetic and inertial ranges. This threshold is independent of heliocentric distance and solar wind conditions. The detailed behaviour of the fluctuations above the threshold varies, reflecting different ways that turbulence develops with distance from the sun. This suggests an underlying mechanism governing these coherent structures that is the same regardless of the specific plasma conditions.
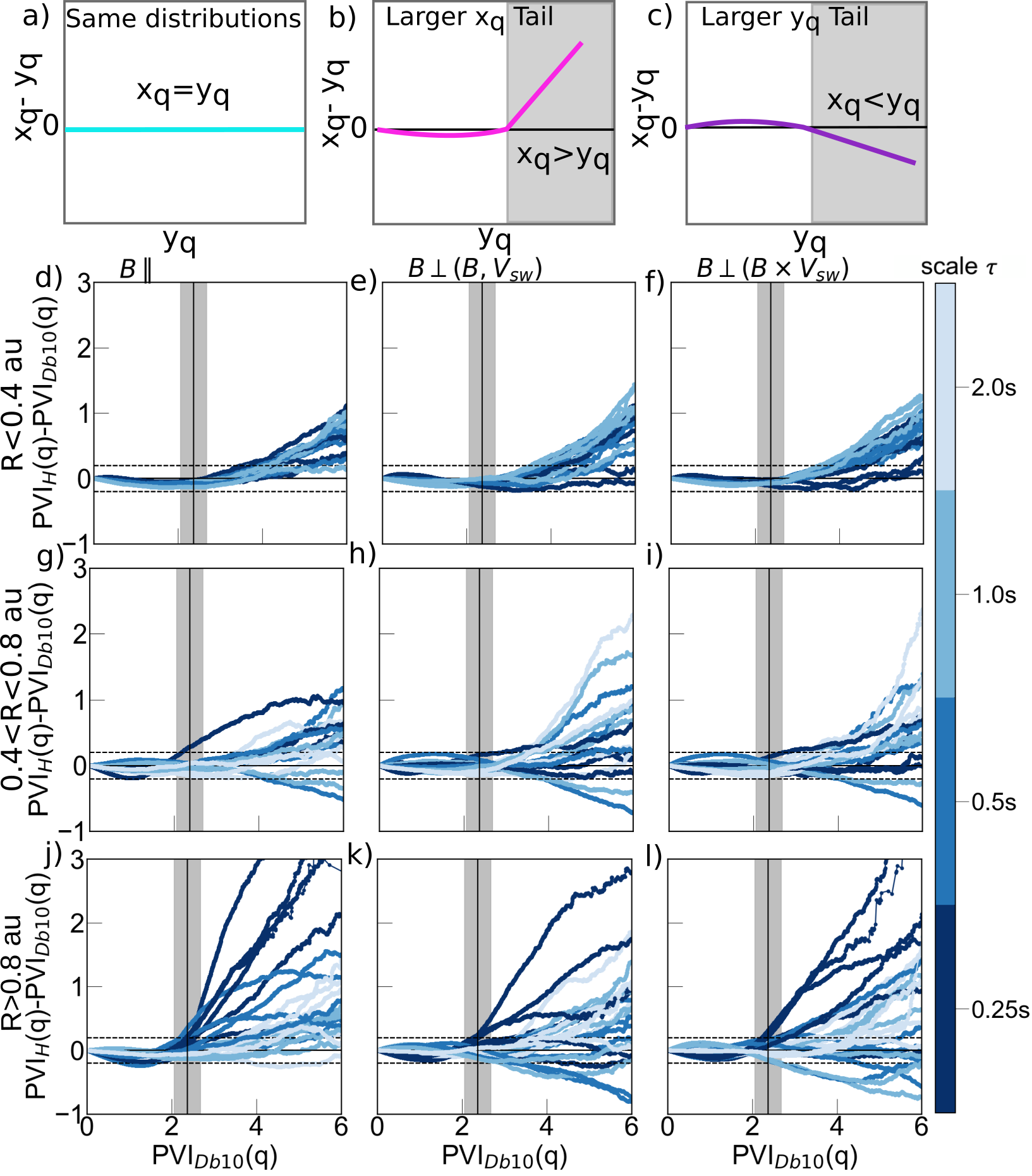
Compensated Quantile-Quantile (QQ) plots discriminate where the Haar (sharp changes) and Db10 (wave-packet) decomposed PVI fluctuation distributions diverge (gray shading) for all solar wind intervals in the kinetic range. The upper panels [(a)–(c)] illustrate the compensated QQ plots. [(d)–(j)] are compensated QQ plots in the kinetic range overplotted for all intervals. These are divided into three categories based on heliocentric distance, (i) 0.3 R < 0.4 au, (ii) 0.4 < R < 0.8 au, and (iii) R > 0.8 au (rows), shown for all magnetic field components (columns). The different scales τ are color coded from dark blue (0.25 s) to light blue (2 s). The overplotted PVI threshold of 2.2 (marked by a black vertical line) is the same for all panels, capturing where the Haar and Db10 derived PVI distributions diverge. The gray shaded region determined from the variance of the threshold ranges from 2.1 to 2.7. This threshold is independent of the scale τ of the turbulence and heliocentric distance. Dashed horizontal lines are at PVI ±0.2 for reference.
See publication for details:
Bendt & Chapman (2025) Ubiquitous threshold for coherent structures in solar wind turbulence, Phys. Rev. Research, doi:10.1103/PhysRevResearch.7.023176